Lectures
Speakers
- Erika Ábrahám
- Christel Baier
- David Basin
- Jasmin Blanchette
- Byron Cook
- Alastair Donaldson
- Ichiro Hasuo
- Marijn Heule
- Laura Kovács
- Assia Mahboubi
- Ruzica Piskac
- Alexandra SilvaProgram
Program
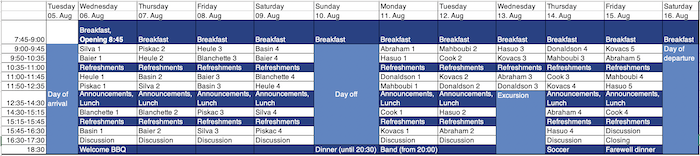
Download program here.
Lectures
The Art of SMT Solving
Erika Ábrahám
SMT (Satisfiability Modulo Theories) solving is a technology for the fully automated solution of logical formulas. SMT solvers can be used as general-purpose off-the-shelf tools. Due to their impressive efficiency, they are nowadays frequently used in a wide variety of applications. A typical application encodes real-world problems as logical formulas, whose solutions can be decoded to solutions of the real-world problem.
Besides its unquestionable practical impact, SMT solving has another great merit: it inspired truly elegant ideas, which do not only enable the construction of efficient software tools, but provide also interesting theoretical insights.
In this lecture series we give an introduction to the mechanisms of SAT and SMT solving, discuss some interesting ideas behind recent developments, and illustrate the usage of SMT solvers on a few application examples.
Probabilistic Model Checking
Christel Baier
Markov chains (MC) and Markov decision processes (MDP) are widely used as operational models for the quantitative system analysis. They can be understood as transition systems augmented with distributions for the states (in MCs) or state-action pairs (in MDPs) to specify the probabilities for the successor states. Additionally one might add weight functions for modeling accumulated costs or rewards earned along path fragments to represent e.g. the energy consumption, the penality to be paid for missed deadlines, or the degree of the achieved utility.
The tutorial will introduce the main features of discrete-time, finite-state Markovian models (MC and MDP) and their
quantitative analysis against temporal logic specifications. The first part will present the basic principles of the
automata-based approach for linear temporal logic (LTL) and probabilistic computation tree logic (PCTL). The second part of the tutorial will present algorithms for the stochastic shortest-path problem. The last part will be about recent trends towards certifying verification algorithms for Markovian models.
Analyzing Cryptographic Protocols with Tamarin
David Basin
The Tamarin prover is a state-of-the-art automated tool for the analysis of cryptographic protocols, which can be used to prove protocol properties and also automatically find attacks. Tamarin has been successfully used to analyze many real-world protocols including TLS 1.3, the mobile communication standard 5G, the EMV chip-and-pin standard, Apple's iMessage Protocol, and many others, leading to the discovery of subtle attacks or automated proofs. In this tutorial, we will introduce Tamarin, its foundation, usage, and applications. Tamarin is open-source software and further information, including the manual, the source code, and scientific papers are available at https://tamarin-prover.com. Participants will be encouraged to try out their knowledge on some simple examples provided in the tutorial.
Saturation-Based Theorem Proving
Jasmin Blanchette
Automatic theorem provers that implement the resolution or superposition calculus are based on saturation: Starting from an initial set of formulas, called clauses, they derive new clauses until a contradiction is found. In this lecture series, (1) I will describe a so-called saturation framework that abstractly captures the workings of saturation provers; (2) I will show how resolution and superposition fit within that framework; (3) I will describe how to extend the framework with clause splitting, an optimization found in Vampire and other state-of-the-art provers; and (4) I will describe Vampire's AVATAR architecture and show that it is an instance of the extended framework.
Cloud Reasoning
Byron Cook
The talks will describe how the existence of the cloud changes the game for formal automated reasoning.
Automated Randomized Testing of Compilers
Alastair Donaldson
In the lecture series I will give an overview of the field of automated compiler testing, focusing on what makes compiler testing difficult - the oracle problem - and discussing various approaches to circumventing the oracle problem, including metamorphic testing and differential testing. I will present some of the most recent, effective techniques in this research field, including some of my own work on automated testing of compilers for GPU programming languages, for the C programming language, and for the Dafny verified programming language.
Abstract and Concrete Model Checking: Through the Lens of Lattice Theory and Category Theory
Ichiro Hasuo
I will sketch a few aspects of lattice theory and category theory that arise in model checking, demonstrating how they are relevant to some recent techniques such as probabilistic verification by ranking supermartingales, compositional model checking, and IC3/PDR. For model checking researchers, the lectures will serve as an introduction to the abstract theories of lattices and categories. The relevance of such theories is the most notable in the unified treatment of qualitative and quantitative model checking. For semantics researchers, the lectures will suggest model checking as a promising application area for their mathematical techniques. In particular, I will introduce some recent results in which abstract theories are exploited for devising fast algorithms.
Mathematics and Symbolic AI
Marijn Heule
Progress in symbolic AI has made it possible to determine the correctness of complex systems and answer long-standing open questions in mathematics. The crucial technology in many successes in computer-aided mathematics is satisfiability (SAT) solving. We highlight some of these successes, including computing Schur number five, the resolution of Keller's conjecture, and solving the empty hexagon problem. The SAT solving approach can produce clever though potentially gigantic proofs. We can have confidence in the correctness of the answers because highly trustworthy systems can validate the underlying proofs regardless of their size. Symbolic AI may well be suitable to solve some notorious math challenges. In particular, we discuss applying these techniques to the Hadwiger Nelson problem (chromatic number of the plane), optimal schemes for matrix multiplication, and the Collatz conjecture.
First-Order Theorem Proving and Vampire
Laura Kovács
First-order theorem proving is one of the earliest research areas within artificial intelligence and formal methods. It is undergoing a rapid development thanks to its successful use in program analysis and verification, security analysis, symbolic computation, theorem proving in mathematics, and other related areas. Breakthrough results in all areas of theorem proving have been obtained, including improvements in theory, implementation, and the development of powerful theorem proving tools. However, recent developments are not always easily accessible to non-specialists.
This mini-lecture series presents the theory and practice behind the development of powerful theorem proving tools. The workhorse used for a demonstration of concepts discussed at the tutorial will be our theorem prover Vampire.
The lectures will first focus on practicalities while using first-order Vampire for validating mathematical theorems. We will then further introduce the core concepts of automating first-order theorem proving in first-order logic with equality. We will discuss the resolution and superposition calculus, introduce the saturation principle, present various algorithms implementing redundancy elimination, and demonstrate how these concepts are implemented in Vampire.
Formal Proofs for Free!
Assia Mahboubi
This series of lectures is concerned with the application of parametricity theorems, from the theory of programming languauges, to interactive theorem proving. The lectures will illustrate how such meta-level properties of the underlying type theory to the theorem prover can be turned into concrete effective tools, e.g., for producing refinement proofs and for producing powerful induction principles.
Privacy-Preserving Automated Reasoning
Ruzica Piskac
In these lectures students will learn how to incorporate cryptographic primitives into automated reasoning. We will present a privacy-preserving Boolean satisfiability solver, which allows mutually distrustful parties to evaluate the conjunction of their input formulas while maintaining privacy. Additionally, we will also show how to prove the unsatisfiability of formulas by using zero-knowledge protocols. We will discuss how the full formal verification workflow can be applied in privacy-preserving settings.
Kleene Algebra with Tests: An Algebraic Approach to Program Verification
Alexandra Silva
Kleene algebra with tests is an algebraic framework that can be used to reason about imperative programs. It has been applied across a wide variety of areas including program transformations, concurrency control, compiler optimizations, cache control, networking, and more. In these lectures, we will provide an overview of NetKAT, a domain specific language based on Kleene Algebra with Tests, and how it can be used as a core framework for network verification.
Downloads
- MOD25_Program (68 KByte)
- Program MOD25 (509 KByte)

